Tabla de Contenido
- Inserción de ecuaciones
- Símbolos matemáticos de utilidad
- Fracciones
- Raíces
- Subíndices y superíndices
- Paréntesis, llaves y corchetes
- Funciones trigonométricas
- Logaritmos
- Sumatorio y productorio
- Integrales
- Límites
- Matrices
- Alineación de ecuaciones
- Vectores
- Acentos
- Texto dentro de una ecuación
- Tipos de letra en el modo matemático
- Referenciar una ecuación
El primer paso para escribir ecuaciones en LaTeX es crear un documento, con el formato y clase que se requiera, y cargar los paquetes necesarios para interpretar los comandos matemáticos. Estos dos pasos pueden llevarse a cabo de forma muy simple con el siguiente código:
\documentclass{article} %Definición del tipo de documento, en este caso artículo
\usepackage{amssymb, amsmath} %Paquetes matemáticos de la American Mathematical Society
\begin{document}
\usepackage{amssymb, amsmath} %Paquetes matemáticos de la American Mathematical Society
\begin{document}
%Aquí escribiremos el contenido del documento. En este caso ecuaciones.
\end{document}
A continuación hay que definir el entorno dentro del cual se incluirá la ecuación. Si la ecuación debe aparecer de forma continua en una línea de texto (modo texto) debe indicarse con los comandos $ … $ o \( ... )\
Por ejemplo, el código:
Dada una función $f(x)=y$, el valor de la variable…
Produce el resultado
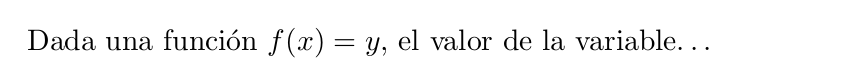
Si, en cambio, queremos que la ecuación aparezca centrada en una línea separada (modo display) debemos utilizar los comandos \begin{equation} … \end{equation} o alternativamente \[...]\
En este caso, el código:
Dada una función
\begin{equation}
el valor de la variable…
\begin{equation}
f(x)=y
\end{equation}el valor de la variable…
Produce el resultado
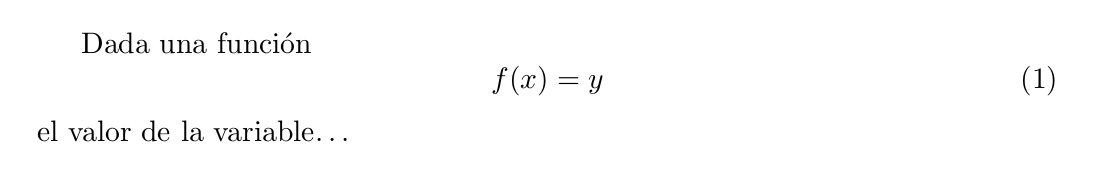
En este caso la ecuación aparece automáticamente numerada. Si no queremos numerar las ecuaciones debemos indicarlo utilizando en su lugar los comandos \begin{equation*} … \end{equation*}
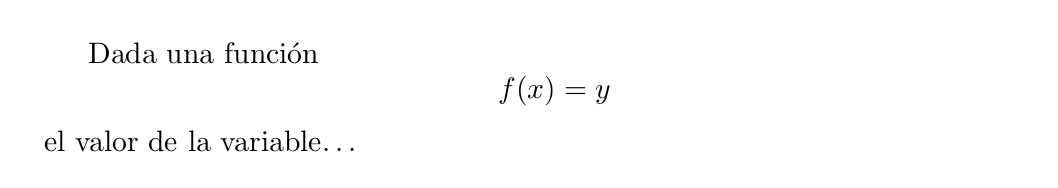
Una vez definidos los delimitadores del entorno equation solo debemos escribir en su interior los comandos referentes a la ecuación en cuestión. Esta puede incluir números, letras, símbolos, operadores, fracciones, matrices, integrales y un largo etcétera.
Símbolos matemáticos de utilidad
Los símbolos matemáticos más habituales (suma, resta, igual, paréntesis, …) pueden escribirse directamente en una ecuación sin necesidad de usar comandos especiales.
Código
(2+3) - 6 = -1
Resultado
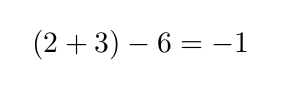
Este es también el caso para los símbolos de desigualdades (< y >).
Código
5 < 7
Resultado
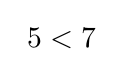
Otros símbolos que podemos escribir directamente son: ! / ( ) [ ] | : *
Para las multiplicaciones podemos utilizar el punto con el comando \cdot o una cruz con el comando \times:
Código
2\cdot 3 = 2\times 3 = 6
Resultado
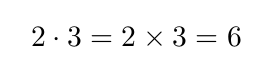
Otros símbolos utilizados habitualmente son los siguientes:
\pm
\approx
\approxeq
\geq
\geqslant
\leq
\leqslant
\neq
\ll
\gg
\equiv
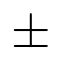
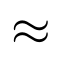
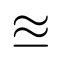
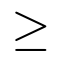
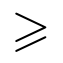
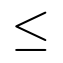
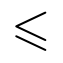
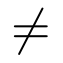
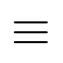
Fracciones
Podemos introducir fracciones con el comando \frac{numerador}{denominador}. Es necesario incluir entre llaves los dos argumentos que requiere este comando, es decir, las expresiones para el numerador y para el denominador.
Código
\frac{120}{527}
Resultado
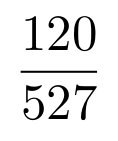
Además del comando \frac también podemos utilizar los comandos \tfrac y \dfrac. \tfrac es el comando de fracciones en estilo texto y \dfrac es el comando en estilo display. Si solo indicamos la fracción con \frac LaTeX se encarga de escoger la versión más adecuada al contexto.
El estilo texto, \tfrac, es de menor tamaño y encaja mejor en ecuaciones escritas a lo largo del texto. Para ecuaciones escritas en una línea separada LaTeX escogerá automáticamente el formato \dfrac, pero solo cuando tenga espacio suficiente para escribir la ecuación entera. En caso contrario, puede escoger utilizar el modo texto. Para sobrescribir estas instrucciones es necesario utilizar \dfrac o \tfrac.
Si en modo texto no indicamos nada (es decir, utilizamos \frac) LaTeX mostrará la ecuación en modo texto.
Dada una función $\frac{79}{88}$ que indica…
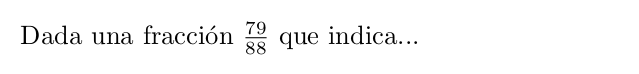
Podemos reescribir esta instrucción indicando que queremos mostrar la ecuación en modo display mediante el comando \dfrac.
Dada una función $\dfrac{79}{88}$ que indica…
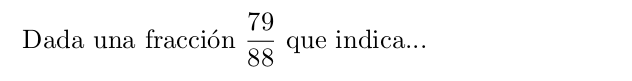
Raíces
La raíz cuadrada puede indicarse con el comando \sqrt:
Código
\sqrt{9} = 3
Resultado
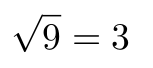
Para introducir otros exponentes simplemente tenemos que indicarlo entre corchetes:
Código
\sqrt[4]{16} = 2
Resultado
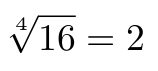
Como puedes ver a continuación, podemos empezar a combinar distintos comandos para crear expresiones más complejas:
Código
\sqrt[3]{\frac{250}{2}} = \sqrt[3]{125} = 5
Resultado
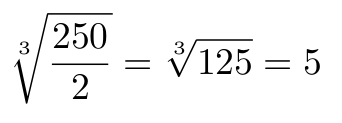
Subíndices y superíndices
Para introducir subíndices solo hay que indicarlo mediante el símbolo _. Por ejemplo
K_n
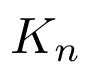
Los superíndices o exponentes se introducen mediante el símbolo ^. Por ejemplo
Código
2^3 = 8
Resultado
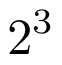
También es posible introducir estos dos elementos simultáneamente
Código
K_n^2
Resultado
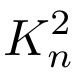
Es importante tener en cuenta que LaTeX asume que el subíndice o superíndice es solamente el carácter situado inmediatamente después del símbolo _ o ^. Así, el siguiente código
2^24
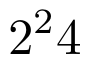
Si queremos introducir un subíndice o superíndice de más de un carácter debemos encerrar todos los caracteres correspondientes entre llaves. En el caso anterior esto sería
Código
2^{24}
Resultado
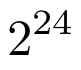
Paréntesis, llaves y corchetes
Los paréntesis y corchetes en LaTeX pueden escribirse directamente, sin necesidad de comandos especiales
Código
(2), [3]
Resultado
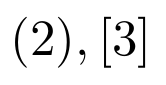
Las llaves también se escriben directamente pero en este caso hay que escribir primero una barra invertida para que LaTeX interprete esta instrucción correctamente
Código
\{8\}
Resultado
Otros tipos de delimitadores de uso habitual son
Código
|3|, \|5\| y \langle 7 \rangle
Resultado
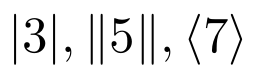
Los paréntesis, llaves y corchetes escritos mediante estos comandos son siempre de tamaño fijo. A veces es necesario insertar estos elementos con un tamaño variable que se adapte a la ecuación que contienen. Como puedes ver en el siguiente ejemplo, sería mejor insertar unos paréntesis con la misma altura que la fracción interior:
Código
(\frac{5}{15})
Resultado
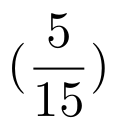
Para indicar que los paréntesis deben tener una altura variable tenemos que insertar los comandos \left y \right antes del paréntesis de la izquierda y derecha, respectivamente. Por ejemplo,
Código
\left(\frac{5}{15}\right)
Resultado
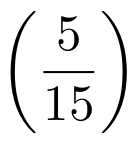
Esto mismo puede aplicarse a las llaves, corchetes y al resto de delimitadores.
Funciones trigonométricas
Aunque es posible escribir directamente funciones trigonométricas dentro de una ecuación (sin, cos, …) LaTeX incorpora una serie de comandos para definir estas funciones correctamente. Normalmente estos comandos consisten en una barra invertida junto con la abreviatura de la función trigonométrica en cuestión. Algunas de las más utilizadas son las siguientes
\sin
\cos
\tan
\arcsin
\arccos
\arctan
\csc
\sec
\cot
\sinh
\cosh
\tanh
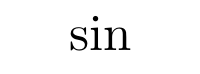
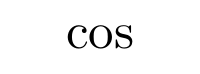
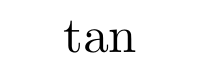
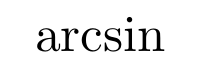
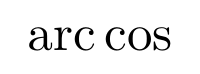
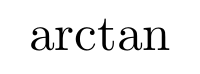
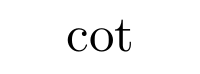
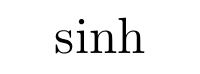
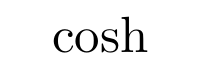
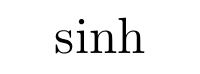
Logaritmos
Como en el caso de las funciones trigonométricas, los logaritmos se indican correctamente mediante los comandos:
\log
\ln
\ln
Sumatorio y productorio
El sumatorio puede insertarse mediante el comando \sum. Para introducir los argumentos de un sumatorio utilizamos la misma notación que para los subíndices y superíndices. Recuerda encerrar todos los caracteres del subíndice o superíndice entre llaves. Por ejemplo,
Código
\sum_{n=1}^{10}n
Resultado
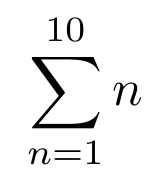
De forma equivalente podemos escribir el símbolo del productorio con el comando \prod.
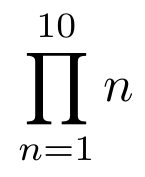
Integrales
Las integrales en LaTeX siguen la misma notación que en el caso del sumatorio o el productorio. Para insertar el símbolo de integral utilizamos el siguiente comando:
\int
A continuación podemos especificar los límites de la integral mediante _ para el límite inferior y ^ para el límite superior.
Código
\int_0^5 x \mathrm{d}x
Resultado
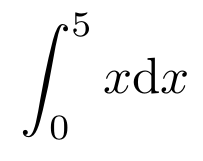
Como puedes ver en el ejemplo anterior la d se engloba dentro del comando \mathrm para que no aparezca en cursiva. Este detalle puede depender del gusto editor pero se considera notación estándar hacerlo de este forma.
Como en el caso del sumatorio, es necesario escribir los límites de la integral entre llaves si tienen más de un carácter:
Código
\int_0^{\infty} x \mathrm{d}x
Resultado
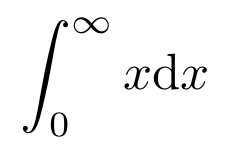
Existen distintas variaciones del símbolo de la integral. Podemos escribir integrales dobles, triples, cuádruples o múltiples mediante los comandos
Código
\iint
\iiint
\iiiint
\idotsint
\iiint
\iiiint
\idotsint
Resultado
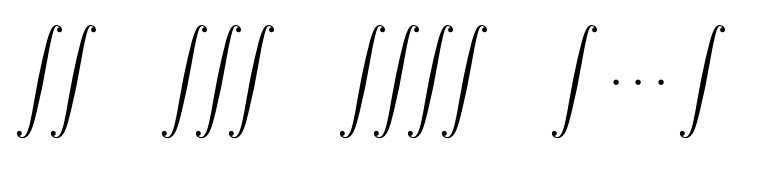
También tenemos disponible el símbolo de una integral a lo largo de una línea cerrada mediante
Código
\oint
Resultado
Límites
La abreviatura correspondiente a límite se inserta en LaTeX mediante el comando \lim. Para especificar los elementos del límite (e.g. cuando x tiende a cero) utilizamos la misma notación que para subíndices.
En estos casos es habitual insertar una flecha para indicar la tendencia de la variable. Esta flecha puede insertarse con el comando \rightarrow o alternativamente con el comando \to.
También es habitual en estos casos insertar el símbolo de infinito, que puede escribirse mediante el comando \infty.
Por ejemplo,
Código
\lim_{x\rightarrow\infty}\frac{3+x}{x^2}
Resultado
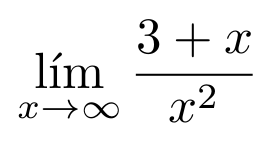
Matrices
Una opción para escribir matrices en LaTeX es utilizar el entorno matrix. En este caso las distintas celdas se separan mediante el símbolo ampersand (&) y cada final de fila se indica mediante doble barra inversa (\\). Con este método podemos crear la siguiente matriz.
Código
\begin{matrix}
5 & 4 & 8 \\
4 & 0 & 7 \\
3 & 5 & 6
\end{matrix}
4 & 0 & 7 \\
3 & 5 & 6
Resultado
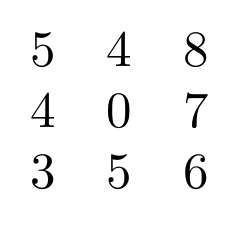
En el caso anterior la matriz aparece sin ningún tipo de delimitador. Si queremos introducir algún tipo de delimitador podemos utilizar variaciones del entorno matrix. Los más habituales son pmatrix, bmatrix, Bmatrix, vmatrix y Vmatrix.
pmatrix
bmatrix
Bmatrix
vmatrix
Vmatrix
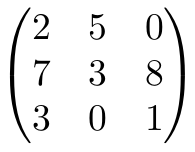
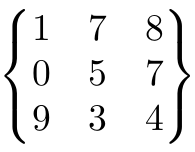
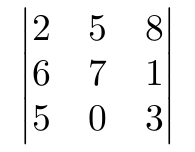
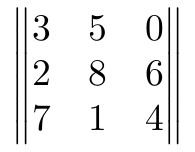
Alternativamente puedes utilizar siempre el entorno matrix e incluir el delimitador que necesitas inmediatamente antes y después de abrir y cerrar este entorno. Por ejemplo
\left(
\begin{matrix}
\right)
\begin{matrix}
5 & 4 & 8 \\
4 & 0 & 7 \\
3 & 5 & 6
\end{matrix}4 & 0 & 7 \\
3 & 5 & 6
\right)
Alineación de ecuaciones
Es habitual encontrarse con ecuaciones o grupos de ecuaciones que ocupan más de una línea. Esto ocurre si la ecuación es demasiado larga para ser escrita en una sola línea o si escribimos distintos pasos a partir de una ecuación inicial. Existen diferentes opciones para dar formato a este tipo de ecuaciones.
Para ecuaciones largas una opción es utilizar el entorno multline en lugar del entorno equation. Este entorno parte la ecuación en el punto donde indiquemos y mantiene un solo número para numerar la ecuación entera.
\begin{multline}
(x+y+z)^3+k = x^3+y^3+z^3 \\
+ 3x^2y + 3x^2z + 3xy^2 + 3y^2z + 3xz^2 + 3yz^2 + 6xyz + k
\end{multline}
+ 3x^2y + 3x^2z + 3xy^2 + 3y^2z + 3xz^2 + 3yz^2 + 6xyz + k
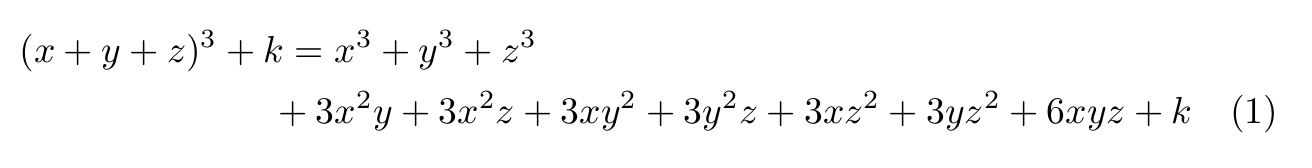
Si queremos tener más control sobre la alineación de cada línea es mejor usar el entorno split dentro de un entorno equation. Dentro de este entorno podemos indicar saltos de línea con \\ y también el punto donde todas las líneas de la ecuación deben alinearse con &. El siguiente ejemplo muestra el funcionamiento de este entorno:
\begin{equation}
\begin{split}
\end{split}
\begin{split}
(a+b)^2& = (a+b)(a+b)\\
& = a^2 + ab + ab + b^2\\
& = a^2 + 2ab + b^2
\end{equation}& = a^2 + ab + ab + b^2\\
& = a^2 + 2ab + b^2
\end{split}
La expresión anterior está compuesta por tres líneas y todas ellas están alineadas en el punto del símbolo “=”. En el caso anterior se asigna un único número para todo el conjunto dentro del entorno split. Si queremos crear una alineación similar pero con un número distinto para la ecuación de cada línea es mejor utilizar el entorno align. Un ejemplo de este caso es:
\begin{align}
((a+b)^2& = a^2 + 2ab + b^2\\
(a-b)^2& = a^2 - 2ab + b^2\\
(a+b)(a-b)& = a^2 - b^2
\end{align}
(a-b)^2& = a^2 - 2ab + b^2\\
(a+b)(a-b)& = a^2 - b^2
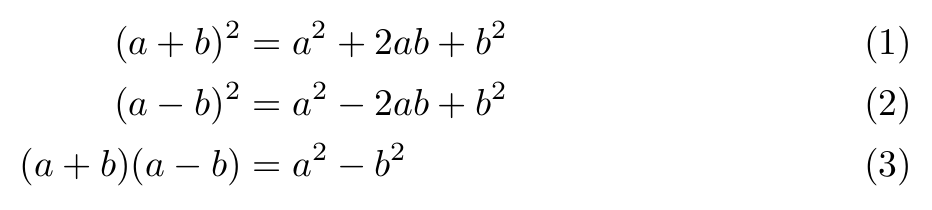
Este entorno funciona exactamente igual que split pero se asigna un número a cada línea.
Otra posibilidad es utilizar el entorno gather. Dentro de este entorno se asigna un número a cada línea y cada ecuación aparece centrada en la página. En este caso no es necesario indicar con el ampersand el punto de alineación. El ejemplo anterior dentro del entorno gather daría el siguiente resultado:
\begin{gather}
((a+b)^2 = a^2 + 2ab + b^2\\
(a-b)^2 = a^2 - 2ab + b^2\\
(a+b)(a-b) = a^2 - b^2
\end{gather}
(a-b)^2 = a^2 - 2ab + b^2\\
(a+b)(a-b) = a^2 - b^2
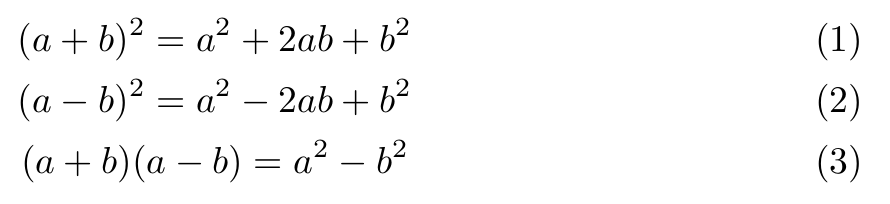
Vectores
Existen una serie de comandos que son indispensables cuando se trabaja con vectores. El primero es sin duda la representación de una pequeña flecha sobre una letra para indicar que se trata de un vector. Esto puede generarse con el comando \vec. Por ejemplo
Código
\vec{v}
Resultado
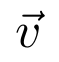
En algunos casos, sobretodo cuando se trata de los vectores unitarios de una base, también se utiliza el acento circunflejo para indicar que se trata de un vector. Este puede insertarse con el comando \hat{}.
Código
\hat{k}.
Resultado
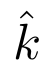
En caso de escribir tres vectores i,j,k combinados con el acento circunflejo es mejor utilizar los comandos \imath y \jmath para la i y la j para sustituir el punto por el acento. Es decir,
Código
\hat{\imath}.
\hat{\jmath}
\hat{k}
\hat{\jmath}
\hat{k}
Resultado
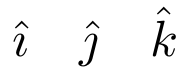
Entre las operaciones más habituales entre vectores tenemos el producto escalar, que podemos representar con \cdot, y el producto vectorial, que podemos representar con \times.
Código
\vec{u}\cdot \vec{v}
Resultado
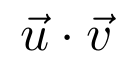
Código
\vec{u}\times \vec{v}
Resultado
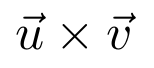
Acentos
Aparte del acento mostrado anteriormente para indicar un vector, existen otros acentos que pueden ser útiles de vez en cuando.
Código
\acute{a}
\grave{a}
\tilde{a}
\bar{a}
\hat{a}
\vec{a}
\dot{a}
\ddot{a}
\dddot{a}
\grave{a}
\tilde{a}
\bar{a}
\hat{a}
\vec{a}
\dot{a}
\ddot{a}
\dddot{a}
Resultado
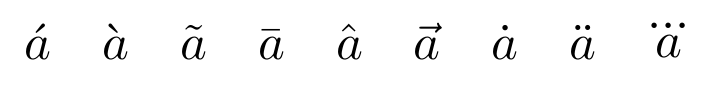
Texto dentro de una ecuación
Existen varias alternativas para insertar texto dentro de una ecuación. Escribir directamente un texto dentro del entorno ecuación no funciona correctamente porque LaTeX interpreta cada carácter como si fuera una variable.
Una primera opción es usar simplemente el comando \text dentro del entorno ecuación para indicar el texto que queremos escribir. Por ejemplo,
\begin{equation}
F = ma \quad\text{Segunda ley de Newton}
\end{equation}
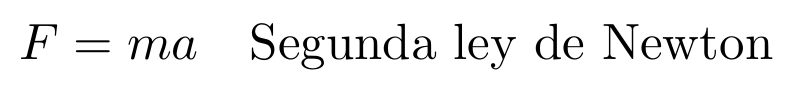
En el ejemplo anterior se ha incluido también el comando \quad para crear un espacio entre la fórmula y el texto. Las variaciones de este comando incluyen \textit para texto en cursiva, \textbf para texto en negrita y \textsf para tipo de letra sans serif.
Si hay que escribir simplemente una letra o palabra puede utilizarse también el comando \mathrm. De forma similar, existen los comandos \mathit para letra cursiva, \mathbf para negrita, \mathsf para letra sans serif y \mathtt para letra de máquina de escribir. Estos comandos no están pensados para escribir texto sino solamente algunas letras en algún tipo de fuente específico. En consecuencia, los espacios son ignorados. A continuación se muestran algunos ejemplos:
Código
f(x) = 2x \quad\mathrm{si}\quad x < 2
f(x) = x^2 \quad\mathit{si}\quad 2 \leq x < 4
f(x) = x + 12 \quad\mathsf{si}\quad x \geq 4
f(x) = x^2 \quad\mathit{si}\quad 2 \leq x < 4
f(x) = x + 12 \quad\mathsf{si}\quad x \geq 4
Resultado
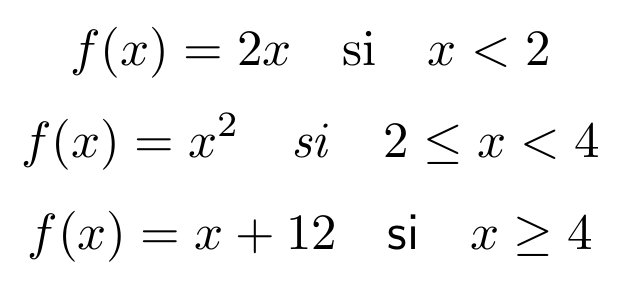
Tipos de letra en el modo matemático
Dentro del modo matemático en LaTeX (por ejemplo, dentro de un entorno equation), a veces es necesario escribir letras con algún tipo de letra distinta. Tres posibilidades muy útiles son las letras caligráficas, las letras negritas de pizarra y las letras Fraktur.
Las letras caligráficas pueden escribirse con el comando \mathcal. Estas son normalmente utilizadas para escribir la transformada de Fourier, \mathcal{F}, o la transformada de Laplace, \mathcal{L}.
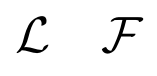
Las letras negritas de pizarra (Blackboard Bold) son muy utilizadas para representar conjuntos de números. Por ejemplo, los números naturales, \mathbb{N}, o los números enteros, \mathbb{Z}.
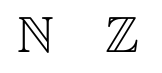
Para otras aplicaciones tenemos también disponible el estilo de letra gótica Fraktur con \mathfrak.
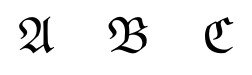
Referenciar una ecuación
Si queremos hacer referencia a una ecuación dentro del texto en primer lugar tenemos que incluir el comando \label dentro de la ecuación correspondiente. El texto dentro del comando label es la etiqueta de la ecuación. Por ejemplo
\begin{equation}
\label{eq:esfera}
V=\frac{4}{3}\pi r^2
\end{equation}
V=\frac{4}{3}\pi r^2
A continuación podemos hacer referencia a esta ecuación en algún punto del texto con el comando \ref. Por ejemplo:
El volumen de una esfera se calcula mediante la ecuación~\ref{eq:esfera}.
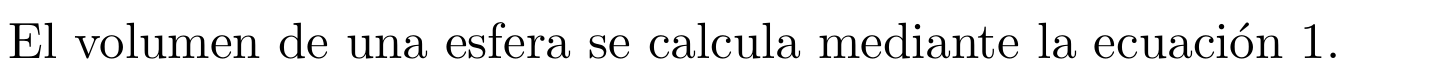
Hay dos detalles importantes en el ejemplo anterior. Uno es que hay que tener en cuenta que se pueden crear etiquetas para otro tipo de elementos (figuras, tablas, etc.). Para mantener un cierto orden dentro del documento es recomendable incluir en el nombre de la etiqueta una referencia al tipo de elemento (fig para figuras, eq para ecuaciones, etc.). En el caso presentado la etiqueta de la ecuación es eq:esfera.
Otro detalle importante es que al hacer referencia a la ecuación se ha escrito el símbolo ~ entre la palabra ecuación y el comando \ref. Esto indica a LaTeX que debe haber un espacio entre los dos elementos pero también que los dos elementos deben estar en la misma línea. Con esto evitamos que haya un salto de línea entre la palabra ecuación y el número de la ecuación.